基于分解的(decomposition-based MOEA)多目标进化算法总结

啰嗦一下：
这一类方法的和核心思想其实是将多目标优化的问题通过参考向量这一方式将其分解为多个单目标的问题，然后对于每个目标，计算对应的解，其解以某种准则进行判断是否对于多目标问题来说是一个优解

一、MOEA/D

参考文献：Q. Zhang and H. Li, “MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition,” in IEEE Transactions on Evolutionary Computation, vol. 11, no. 6, pp. 712-731, Dec. 2007, doi: 10.1109/TEVC.2007.892759.

1、生成参考/权重向量(reference vector/weight vector)

将多目标优化以某种方式分解成多个单目标问题，每个单目标问题的形式如下：

f(x)=∑i=1mλifi(x)f(\bm {x})=\sum _{i=1} ^m {\lambda _i f_i(\bm {x})}

其中λ\lambda满足∑λi=1\sum {\lambda_i}=1
实现这一步的方式通常就称为生成参考向量。一般可以使用标准边界交叉法（nomal boundary intersection NBI）来生成。对于一个mm目标的问题，假设每个目标被划分为HH份，则所有的可能划分组合为

n=(m+H−1m−1)n=\begin{pmatrix} m+H-1 \\ m-1 \\ \end{pmatrix}

在选定mm和HH之后可以得到一个各个目标的权重配比，构成目标空间的参考向量，这里得到的nn就是分解得到的子问题的个数，而对应的每一种组合就是子问题的构成。

2、聚合方法

此时问题就变成了对于单目标的优化，但关键是如何将这些单目标问题的解聚合起来，一般有以下三种聚合方法：
2-0、基于加权权重的方法（对于非凸的问题效果不佳，所以没有详述）
2-1、切比雪夫分解

gtch(x∣λ,z∗)=max1≤i≤m{λi⋅∣fi(x)−zi∗∣}\quad g^{tch}({\bm {x} }| \bm {\lambda },\bm {z^*})=\underset {1 \leq i \leq m} {max} \{ \lambda _i \cdot| f_i({\bf {x} })-z_i^*|\}

这个函数就是在整个目标空间里，取所有权重向量和目标函数与当前参考点的差值乘积的最大值，如果这个最大值都偏向最小，那么其他解就更偏向最小，因此选择这个函数最小的解可以作为最接近PF的解。

2-2、基于惩罚的边界交叉方法（PBI）

gpbi(x∣λ,z∗)=d1+θd2\quad g^{pbi}({\bm {x} }| \bm {\lambda},\bm {z^*})=d_1+\theta d_2

d1=∣∣(z∗−F(x))Tλ∣∣∣∣λ∣∣d_1=\frac {||(z^* -F({\bf {x} }))^T {\bf {\lambda} }||} {||{\bf {\lambda} }||}

d2=∣∣F(x)−(z∗−d1λ)∣∣d_2=||F({\bf {x} })-(z^*-d_1{\bf {\lambda} })||

θ\theta是预设参数，对该方法的准确性有较大的影响，这里的d1d_1和d2d_2分别用于控制生成的解的分布性和收敛性

3、具体步骤

1）初始产生一个种群，设定种群个体数目N，那么就在目标空间中均匀生成N个参考向量，每个参考向量作为一个子问题,每一个个体与且仅与一个参考向量相关联（这里要如何实现？），每个个体对应的目标值向量FVi=F(xi)FV_i=\bm {F(\bm {x_i})}

2）对于每一个参考向量λi\lambda_i，根据其与其他参考向量的欧氏距离可以对每一个参考向量确定T个邻居，则其邻域为NSi={λi1,λi2,...,λiT}{NS}_i=\{\lambda_{i_1},\lambda_{i_2},...,\lambda_{i_T}\}

3）计算理想点作为当前的参考点，zi∗=minx∈Ω{fi(x)}i=1,2,...,mz_i^{*}=\underset {\bm{x} \in \Omega} {min} \{ f_i({\bf {x} })\} \quad i=1,2,...,m，Ω\Omega为决策向量的取值空间。
如果问题的理想点是可以求出的，这里是个定值；如果计算复杂或是无法求出定值，可以由其他方法进行近似

4）对每个参考向量λi\lambda_i，循环进行如下步骤：

  • 在其邻域NSi{NS}_i内随机选择两个个体，进行遗传生成子代x\bm{x}
  • 进行解的改进：使用基于benchmark的方法对生成的解x\bm{x}进行改进得到x′\bm{x}'（这一步如何实现？）
  • 更新参考点:for  j=1,2,...,m,if  zj∗<fj(x′),then  zj∗=fj(x′)for \;j=1,2,...,m,\quad if \;z_j^*<f_j(\bm {x'}),\quad then\; z^*_j=f_j(\bm {x'})
  • 更新邻域：for  j∈NSi,if  gtch(x′∣λ,z∗)≤gtch(xj∣λ,z∗)（切比雪夫）or  gpbi(x′∣λ,z∗)≤gpbi(xj∣λ,z∗)（PBI方法）,then  xj=x′,FVj=F(x′)for \; j \in {NS}_i,\quad if\; g^{tch}({\bm {x}'}| \bm {\lambda },\bm {z^*})\leq g^{tch}({\bm {x_j} }| \bm {\lambda },\bm {z^*})（切比雪夫）or \;g^{pbi}({\bm {x}'}| \bm {\lambda },\bm {z^*})\leq g^{pbi}({\bm {x_j} }| \bm {\lambda },\bm {z^*})（PBI方法）,\quad then \;\bm{x_j}=\bm {x'},FV_j=\bm {F}(\bm {x'})
  • 更新外部EP：一开始是一个空集，将其中被x′\bm{x'}支配的个体移除，如果EP中不存在支配x′\bm{x'}的个体，就将x′\bm {x'}加入EP中

5）迭代多次直至达到结束条件

二、RVEA(reference vector-guided EA)

参考文献：R. Cheng, Y. Jin, M. Olhofer and B. Sendhoff, “A Reference Vector Guided Evolutionary Algorithm for Many-Objective Optimization,” in IEEE Transactions on Evolutionary Computation, vol. 20, no. 5, pp. 773-791, Oct. 2016, doi: 10.1109/TEVC.2016.2519378.

1、生成参考/权重向量(reference vector/weight vector)

参考一-1

2、具体步骤

1）在目标空间中均匀生成N个参考向量V0={v1,0,v2,0,...,vN,0}\bm{V}_0=\{\bm{v}_{1,0},\bm{v}_{2,0},...,\bm{v}_{N,0}\}
2）随机生成初始种群P0P_0，其大小为NN
fort<tmaxfor\quad t<t_{max}
3）在种群中随机进行交叉和变异生成子代，合并父代与子代种群得到中间种群PtP_t
4）对于PtP_t中的每一个个体ii，对应一个目标值向量fi,t\bm {f}_{i,t}，进行一个转换fi,t′=fi,t−zt∗{\bm {f}_{i,t} }'=\bm {f}_{i,t}-\bm {z}_t^{*}，zt∗=minx∈Ω{fi(x)}i=1,2,...,m\bm {z}_t^{*}=\underset {\bm{x} \in \Omega} {min} \{ \bm {f}_i({\bf {x} })\} \quad i=1,2,...,m
5）目标空间被N个参考向量分为N个子种群，对于PtP_t中每一个个体，计算其与所有参考向量的夹角，将其分配给与其夹角最小参考向量所代表的子种群

img

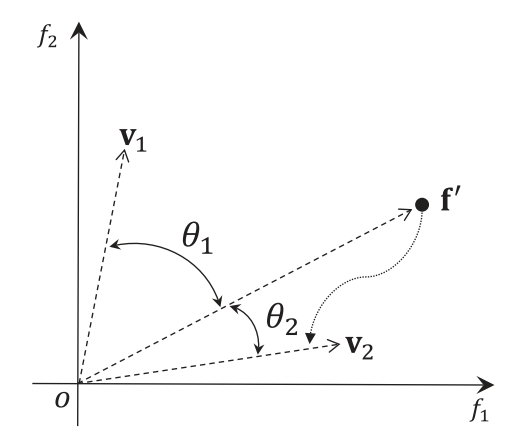
6）对于每一个子种群Pj,j∈{1,2,...,N}P_j,j\in \{1,2,...,N\}，依次计算其中每个个体的APD（angel penalty distance）值，选出最小的个体作为该子种群的最优个体被保留

APD=di,j,t=(1+P(θi,j,t))⋅∣∣fi,t′∣∣APD=d_{i,j,t}=(1+P(\theta _{i,j,t}))\cdot ||{\bm {f}_{i,t} }'||

P(θi,j,t)=m⋅(ttmax)α⋅θi,j,tγvt,jP(\theta _{i,j,t})=m\cdot {(\frac {t}{t_{max} })}^\alpha \cdot \frac {\theta _{i,j,t} }{\gamma _{ {\bm {v}_t},j} }

γvt,j=mini∈{1,2,...,N},i≠j(vi,t,vj,t)\gamma _{ {\bm {v}_t},j}=\underset {i \in \{1,2,...,N\},i \neq j}{min}(\bm {v}_{i,t},\bm {v}_{j,t})

α\alpha是一个超参数，由用户定义

7）对于每个问题归一化后的规模相同的多目标问题上述方法已经可以，但是如果在进行归一化之后各个目标的范围并不一致的情况，这里使用了一个参考向量的自适应改变方法。
在第t代时，我们可以有初始的参考向量V0={v1,0,v2,0,...,vN,0}\bm{V}_0=\{\bm{v}_{1,0},\bm{v}_{2,0},...,\bm{v}_{N,0}\}和第t代的参考向量Vt={v1,t,v2,t,...,vN,t}\bm{V}_t=\{\bm{v}_{1,t},\bm{v}_{2,t},...,\bm{v}_{N,t}\}
if(ttmax)  mod  fr==0,  thenif\quad (\frac {t}{t_{max} })\;mod \;f_r==0,\;then
fori∈{1,2,...N}\qquad for\quad i \in\{1,2,...N\}
vi,t+1=vi,0∘(zt+1max−zt+1min)∣∣vi,0∘(zt+1max−zt+1min)∣∣\qquad\bm {v}_{i,t+1}=\frac {\bm{v}_{i,0}\circ(\bm{z}_{t+1}^{max}-\bm{z}_{t+1}^{min})}{||\bm{v}_{i,0}\circ(\bm{z}_{t+1}^{max}-\bm{z}_{t+1}^{min})||}
elseelse
vi,t+1=vi,t\qquad \bm {v}_{i,t+1}=\bm {v}_{i,t}
这里的∘\circ表示同阶矩阵的逐元素相乘

end  forend \;for